Electronique Mag - Le journal de l'électronique.
- accueil .
- abonnement .
- newsletter .
Flux RSS . - soumissions .
- publicité .
- contacts
Flux RSS .
Les défis sont le circuit de filtrage et d’adaptation auquel l’antenne NFC est connectée. La communication en champ proche (NFC) est une technologie de communication sans fil à courte portée, à haute fréquence et à faible bande passante, qui permet une communication normalisée entre deux dispositifs mobiles tels que des smartphones, des cartes à puce, des autocollants ou des étiquettes. La technologie NFC jouit d’une grande popularité car elle peut être utilisée avec les smartphones. Contrairement aux normes RFID comparables sur la même fréquence de 13,56 MHz, elle est mieux adaptée aux applications sensibles telles que la communication de données et les transactions financières sécurisées grâce à sa courte portée de moins de 10 cm.
Il est complexe de calculer la conception du circuit de filtrage et d’adaptation pour une application NFC. Plusieurs itérations peuvent être nécessaires en raison des tolérances des matériaux des composants. La conception de ce circuit est le sujet ci-dessous.
L’adaptation d’impédance conjuguée complexe est une technique très importante dans la conception de circuits RF. Elle est conçue pour assurer le transfert de puissance maximal possible entre une source et sa charge et pour minimiser les réflexions du signal sur la charge. Un exemple du besoin de transfert de puissance peut être trouvé dans le front-end de tout récepteur sensible.
Il est clair que des pertes inutiles ne peuvent être tolérées dans un circuit qui transporte déjà des niveaux de signal extrêmement faibles. C’est pourquoi, lors de la conception initiale d’un tel front-end, il faut faire très attention à ce que chaque dispositif de la chaîne soit adapté à sa charge. En ingénierie haute fréquence, les charges sont souvent complexes, c’est-à-dire qu’elles ont une composante inductive ou capacitive en plus de leur composante résistive. Pour l’adaptation, la composante inductive ou capacitive doit être compensée par sa contrepartie : la composante dite conjuguée complexe.
Par exemple, cela signifie qu’un composant inductif doit être compensé de manière capacitive.
L’adaptation de l’impédance est basée sur le théorème du transfert de puissance maximale. Elle stipule que pour obtenir la puissance externe maximale d’une source ayant une résistance interne finie, la résistance de la charge doit être égale à la résistance de la source vue depuis ses bornes de sortie. En outre, elle stipule que chaque composante réactive de la source et de la charge doit être égale en magnitude mais de signe opposé. Cela signifie que les impédances de la charge et de la source doivent être conjuguées complexes entre elles. [2]
En général, le conjugué complexe de l’impédance Z = R + jX est Z* = R - jX, où R est la partie réelle et X la partie imaginaire de l’impédance complexe Z. La figure 1 montre l’impédance de source complexe ZS et l’impédance de charge complexe ZL.
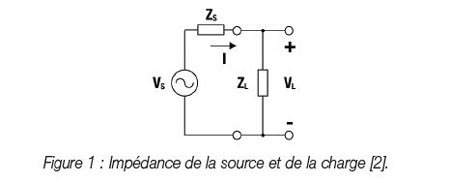
Ces impédances doivent répondre à la condition suivante pour conduire à une correspondance optimale :
De nombreuses topologies de circuit peuvent être utilisées pour réaliser l’adaptation d’impédance. La plus simple est la topologie en L, qui consiste en deux réactances. Cette topologie tire son nom de l’orientation des composants, qui ressemble à la forme d’un L. [1] La figure 2 montre les deux topologies en L possibles pour l’adaptation d’impédance.
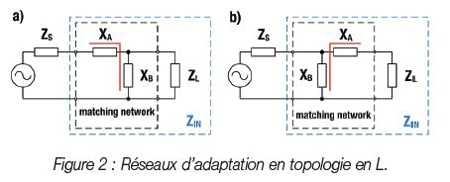
Dans la figure 2, XA est la réactance idéale de la branche série et XB est la réactance idéale de la branche parallèle. ZS et ZL sont les impédances de source et de charge. ZIN désigne l’impédance d’entrée et comprend l’impédance de charge et d’adaptation, qui doit être le conjugué complexe de ZS. Avant de pouvoir déterminer les composants d’adaptation, il faut connaître les impédances de la charge et de la source. L’impédance de la source est de 50 Ω dans la plupart des cas. En général, l’impédance de la source peut également être complexe.
L’impédance de charge complexe peut être déterminée par mesure et calcul. La mesure de l’impédance complexe pour la gamme 13,56 MHz peut être effectuée avec un analyseur de réseau vectoriel qui mesure les paramètres S de l’appareil à tester.
Les paramètres S décrivent le comportement électrique des réseaux électriques linéaires lorsqu’ils sont exposés à différents signaux électriques stationnaires. Pour l’adaptation d’impédance, on utilise le paramètre S11, qui est appelé facteur de réflexion d’entrée. Le facteur de réflexion d’entrée est une quantité complexe dont la valeur absolue est un indicateur de la réflexion. |S11| = 0 signifie que le circuit est parfaitement adapté et qu’aucune des « ondes de puissance » incidentes n’est réfléchie. |S11| = 1 signifie que 100 % de « l’onde de puissance » incidente est réfléchie vers l’entrée. Dans les applications NFC, la charge est une antenne. Pour les calculs pratiques et les simulations, les propriétés électriques de l’antenne sont représentées dans un schéma de circuit équivalent. Le circuit équivalent série simplifié d’une antenne NFC est illustré à la Figure 3.
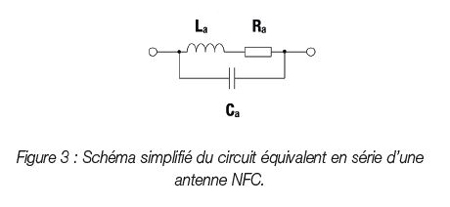
La est l’inductance et Ra est la résistance série équivalente représentant toutes les pertes ohmiques de l’antenne. Ca est la capacitance équivalente parallèle de l’antenne. Les valeurs La et Ra peuvent être mesurées directement avec un analyseur de réseau ou un compteur LCR.
La valeur Ca est une valeur parasite et doit être déterminée par mesure et calcul. Les dépendances en fréquence de La, Ca et Ra ne sont pas prises en compte dans les calculs et les simulations. Si l’inductance La est connue, la capacitance équivalente parallèle Ca à la fréquence de résonance fres peut être calculée avec la formule (2). [8]
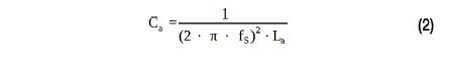
La fréquence de résonance fres est le premier point de mesure où l’impédance de charge complexe devient réelle.
L’impédance de l’antenne ZL, qui est nécessaire pour l’adaptation d’impédance, peut être calculée comme suit :
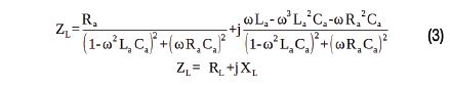
Le facteur de qualité QL de l’antenne est défini par le rapport entre la partie imaginaire XL et la partie réelle RL de l’impédance de l’antenne et peut donc être calculé avec l’équation (4).
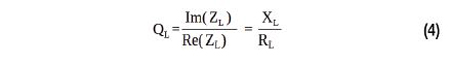
La procédure d’adaptation peut être effectuée par calcul et simulation. En général, les deux réseaux d’impédance présentés à la Figure 2 peuvent être utilisés, mais le réseau présenté à la Figure 2a est plus facile à calculer et a été choisi pour démontrer la procédure d’adaptation. Comme la charge a un comportement inductif, les réactances XA et XB sont capacitives. En général, XA et XB peuvent également être inductifs si la charge a un comportement capacitif. XA et XB sont considérés comme idéaux, c’est-à-dire qu’ils sont supposés ne pas avoir de composant résistif ou parasite.
Pour le réseau illustré à la Figure 2a, la correspondance parfaite est atteinte pour Zin = ZS*. Zin peut être calculée comme suit [5] :
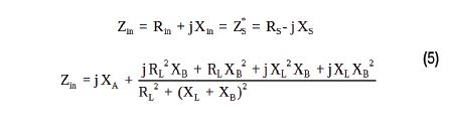
En tenant compte de l’équation (5), on obtient Zin pour les parties réelle et imaginaire de l’impédance d’entrée :
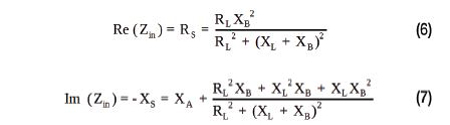
Si l’équation (6) est résolue pour la réactance XB, deux valeurs différentes XB1 et XB2 sont obtenues car (6) est une équation quadratique :
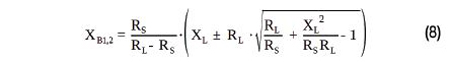
La réactance XA a également deux valeurs, XA1 et XA2, et sur la base de l’équation (7), en tenant compte de l’équation (8), on obtient l’expression suivante :
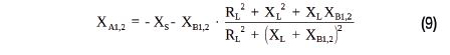
La difficulté de permettre à un appareil de communiquer via NFC réside dans le réseau de filtrage et d’adaptation de l’antenne NFC. La première partie de cet article a présenté la théorie de l’adaptation d’impédance conjuguée complexe. La suite va se concentrer sur l’application de l’adaptation d’impédance à un circuit de sortie NFC. Une bobine combinée alimentation sans fil/NFC de Würth Elektronik est choisie à titre d’exemple.
Commençons par la structure d’un circuit de sortie NFC typique. Un circuit intégré NFC possède généralement une sortie différentielle et une impédance de 50 Ω entre les broches de sortie TX1 et TX2. Ces broches sont connectées à un circuit composé d’un réseau de filtrage, d’un circuit d’adaptation, de résistances d’atténuation et d’une antenne NFC. La sortie du circuit intégré NFC est différentielle pour assurer la résistance aux interférences électromagnétiques. Un circuit de sortie NFC différentiel typique est illustré à la Figure 4.
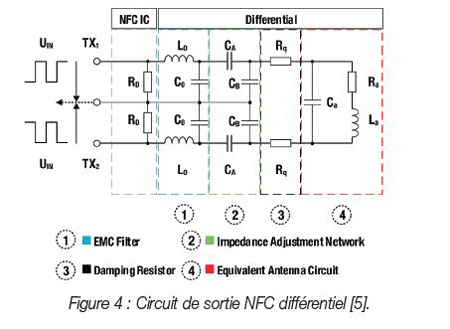
Pour simplifier la compréhension des composants du circuit de sortie NFC, le circuit différentiel peut être converti en un circuit asymétrique. Les équations (8) et (9) peuvent être appliquées pour calculer les condensateurs d’adaptation CA et CB. Les calculs de transformation sont effectués comme dans [6] et le circuit asymétrique résultant est illustré à la Figure 5.
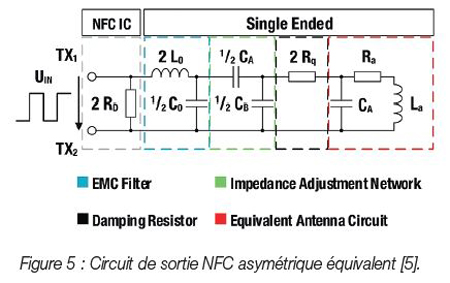
Comme le signal de sortie du circuit intégré NFC a une forme rectangulaire, les harmoniques doivent être filtrées. Cette fonction est assurée par le réseau de filtrage CEM, qui constitue un filtre passe-bas de deuxième ordre. Le filtre passe-bas est constitué de l’inductance L0 et de la capacitance C0. La fréquence de coupure fC du filtre CEM peut être calculée avec l’équation (10).
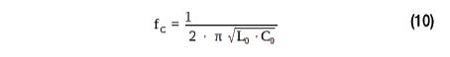
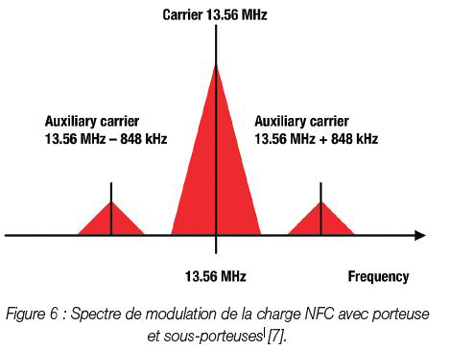
La fréquence de coupure fC doit être supérieure à la sousporteuse supérieure, qui, pour le débit de données NFC le plus élevé possible (848 kbit/s), est de 13,56 MHz + 848 kHz = 14,4 MHz. Pour illustrer la nécessité du filtre, la Figure 6 montre un spectre de modulation de charge NFC avec porteuse et sous-porteuses.
Afin de réaliser l’adaptation d’impédance, l’impédance du filtre doit être calculée à l’aide de l’équation (11).
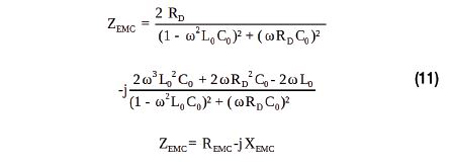
Le circuit d’adaptation, également appelé réseau d’adaptation d’impédance, comme le montrent les Figures 5 et 6 (partie 1), a deux tâches. La première est de compenser l’impédance inductive de l’antenne. La seconde est de réaliser la transformation d’impédance de l’impédance de charge à l’impédance de source. Pour une transformation sans perte, tous les composants doivent être des éléments réactifs. Dans un environnement où les coûts et l’espace sont critiques, comme c’est le cas pour les circuits NFC, il est souhaitable de maintenir le nombre de composants au minimum, et il faut donc utiliser une topologie d’adaptation en L.
La résistance d’amortissement Rq est une résistance optionnelle qui peut être utilisée pour réduire le facteur Q de l’antenne. Le choix de la valeur optimale de Rq est un compromis. D’une part, une petite valeur augmente l’efficacité de l’antenne pour la transmission d’alimentation sans contact ; d’autre part, une valeur de résistance élevée fournit une largeur de bande plus importante pour la modulation et réduit le facteur Q de l’antenne. La plage de valeurs recommandée pour le facteur Q est comprise entre 20 et 35, comme suggéré dans [8]. La résistance Rq doit être utilisée lorsque le facteur Q de l’antenne, qui peut être calculé à l’aide de l’équation (4), dépasse 35. Si la valeur est supérieure, l’équation (4) doit être modifiée à l’aide de l’équation (12). [5]
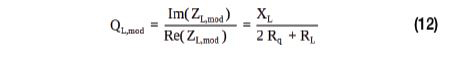
Il en résulte la formule suivante pour calculer la valeur de la résistance d’amortissement Rq (pour QL,mod ≥ 35) :
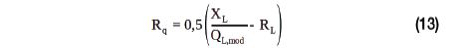
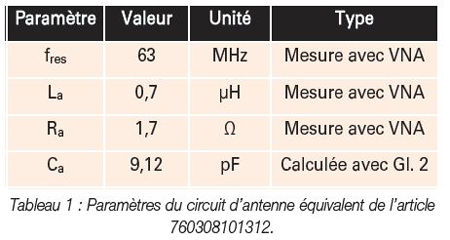
La dernière partie du réseau de sortie est le circuit d’antenne équivalent décrit dans la première partie de cette série. Ce réseau a été utilisé pour les simulations et les calculs de l’impédance de la charge.
Pour l’antenne NFC WE-WPCC WPT/NFC (article 760308101312), les paramètres donnés dans le tableau 1 ont été déterminés par mesure et calcul.
Les valeurs pour La et Ra ont été mesurées à la fréquence de fonctionnement prévue de 13,56 MHz.
L’impédance complexe ZL de l’antenne NFC de l’article WE-WPCC WPT/NFC (760308101312) est calculée avec l’équation (3) en insérant les paramètres du circuit d’antenne équivalent déterminés dans la section précédente, ce qui donne la valeur d’impédance complexe suivante.
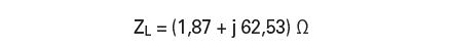
Sur la base de l’équation (4), cela conduit à un QL de 33. Comme le facteur Q de l’antenne est inférieur à 35, les résistances d’amortissement Rq peuvent être omises.
Pour la fréquence de coupure fC, qui peut être calculée à l’aide de l’équation (10), une valeur de 14,8 MHz a été choisie, qui est supérieure à 14,4 MHz. Pour L0, une valeur d’inductance de 470 nH est choisie, ce qui donne une C0 de 247 pF. Les valeurs L0 et C0 doivent être substituées dans l’équation (11) pour calculer l’impédance complexe du filtre. Pour RD, la valeur de 25 Ω est insérée, ce qui correspond à l’impédance de sortie différentielle d’un circuit intégré NFC typique par rapport au signal de masse.
Ces valeurs donnent l’impédance complexe suivante du filtre :
Les réactances d’adaptation XB et XA peuvent être calculées directement avec les équations (8) et (9). Pour RS, il faut utiliser la partie réelle du réseau CEM, qui est de 165,82 Ω. Pour la partie imaginaire de la réactance de la source XS, il faut utiliser la partie imaginaire du filtre CEM, qui est de -45,46 Ω. Pour RL et XL, il faut intégrer les parties réelles et imaginaires du réseau de l’antenne, à savoir 1,87 Ω et 62,53 Ω.
Les réactances d’adaptation résultantes XA et XB peuvent être converties en condensateurs d’adaptation différentiels correspondants CA et CB comme suit :
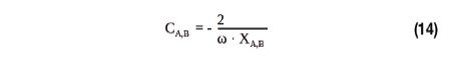
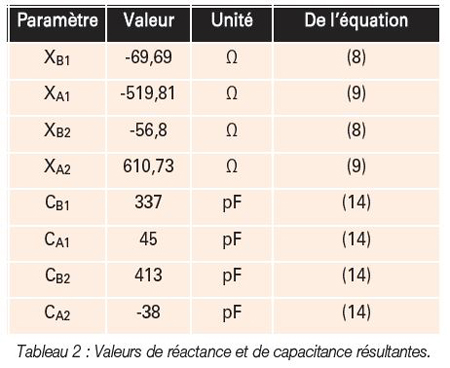
Le Tableau 2 donne un aperçu des valeurs de réactance et de capacitance obtenues.
Les valeurs des condensateurs CA1 et CB1 sont utilisées pour l’adaptation ; les valeurs de CA2 et CB2 sont négligées car CA2 donne une valeur négative. Il en résulte les condensateurs d’adaptation pour le circuit de sortie différentiel à :
CA = 45 pF
CB = 337 pF
Pour vérifier si les valeurs calculées des condensateurs d’adaptation CA et CB donnent lieu à une faible réflexion, le paramètre S11 doit être calculé à la sortie du circuit intégré NFC. Plus les valeurs absolues sont petites, plus la réflexion est faible et plus le circuit est bien adapté à l’impédance de sortie de 50 Ω du circuit intégré NFC.
Le facteur de réflexion d’entrée complexe S11 peut être calculé à l’aide de la formule (15).
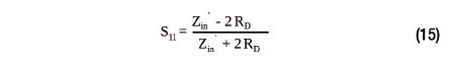
où RD = 25 Ω, qui correspond à l’impédance de sortie asymétrique du circuit intégré NFC. Le paramètre Zin’ dépend de l’impédance d’entrée Zin (voir l’équation (5)) et peut être calculé avec la formule (16).
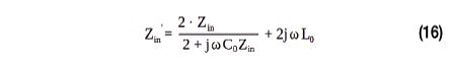
La quantité de S11 peut être calculée avec :
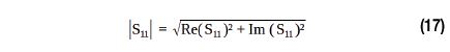
Dans la technologie des hautes fréquences, |S11| est souvent donné sur une échelle logarithmique et peut être calculé comme suit :
Les valeurs résultantes des équations (5) et (15)-(18) sont présentées dans le Tableau 3.
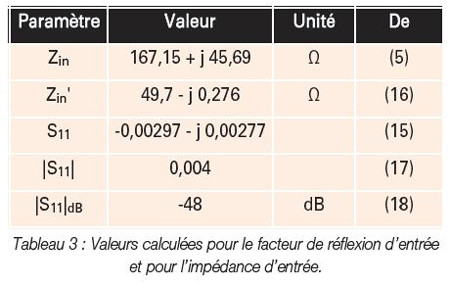
Les calculs sont effectués avec des composants idéaux, sans tenir compte des influences parasites et des tolérances. Cependant, en réalité, les condensateurs et les inductances ont des tolérances et des inductances et des capacitances parasites. Souvent, ces valeurs parasites sont utilisées comme partie du réseau d’adaptation/filtrage. En outre, les composants du circuit équivalent de l’antenne sont mesurés et ne sont donc pas précis, ils ont donc également des tolérances. Outre les variations géométriques et chimiques causées par le processus de fabrication, il existe également des paramètres inconnus de l’environnement ou des feuilles de ferrite ajoutées pour le blindage. Tout métal à proximité de l’antenne peut modifier l’impédance de l’antenne et donc aussi l’impédance d’entrée totale. La mesure dans laquelle ces variations affectent l’impédance d’entrée dépend principalement de la valeur de l’impédance d’entrée et du facteur de qualité. En général, les facteurs de qualité plus faibles et les valeurs d’impédance d’entrée plus élevées sont moins sensibles à une variation des valeurs des composants. [5] Compte tenu de ces variations, une itération supplémentaire de l’ajustement est nécessaire.
Nous avons décrit comment une antenne NFC WE peut être adaptée à un circuit intégré NFC. La détermination des valeurs des condensateurs d’adaptation a été calculée et la mesure et l’adaptation nécessaire de l’impédance d’entrée à l’impédance de la source ont été montrées.
Les bases de la théorie de l’adaptation d’impédance complexe ont été présentées dans la première partie de l’article et des topologies typiques d’adaptation en L ont été décrites. Les réactances d’adaptation et la détermination du facteur Q ont été calculées. Les différentes parties du réseau de sortie différentiel ont été analysées, et les différents composants du filtre ainsi que les composants équivalents de l’antenne ont été dimensionnés.
Références :
[1] C. Bowick : RF Circuit Design, 2nd Revised edition, Newnes, 2007.
[2] K. Cartwright, Non-Calculus Derivation of the Maximum Power Transfer Theorem, Technology Interface, 8 (2), 2008.
[3] M. Roland : Automatic Impedance Matching for 13.56MHz NFC Antennas, 6th International Symposium on Communication Systems, Networks and Digital Signal Processing, 2008.
[4] Würth Elektronik eiSos : ANP057a, WE-MCA Multilayer Chip Antenna Placement & Matching, Application Note, 2018.
[5] T. Baier : Automated Impedance Adjustment of 13.56MHz NFC Reader Antennas, Master Thesis, 2014.
[6] A. Schober, M. Ciacci, and M. Gebhart : An NFC Air Interface coupling model for Contactless System Performance estimation, International Conference on Telecommunications (ConTEL), June 2013.
[7] Rohde et Schwarz : Near Field Communication (NFC) Technology and Measurements, White Paper, 2011.
[8] NXP Corporation : AN11564, Antenna Design and Matching Guide, Application Note, 2016.
